中微幼教版（应该）：03 决策论（2） 消费者选择理论

我们上次了解了作为一个人，我们的偏好和对偏好的实现的一些简单的办法。今天我们继续深入这个话题，讨论一下当你足够了解你自己的时候，你会在不同的情况下进行怎样的消费。

消费者选择的几个部分 ​

显然我们要做选择是需要一些条件的，我们想想自己在做一个选择决策的时候会考虑一些什么事情？

偏好 ​

你做选择时会考虑自己的偏好，会在喜之郎果冻和旺旺仙贝里面挑一挑，而不是闭眼拿一个。

价格 ​

某一天旺旺仙贝突然停产被炒到天价，这个时候你的选择和之前的选择还会一样吗？

收入 ​

你的收入只能买一个喜之郎果冻，但是可以买五个旺旺仙贝，这个时候你的选择和你在不考虑收入时候的选择一样吗？我们一般用$m$表示收入。

预算 ​

英文名为Budget，我们用预算来形容能否付得起某一个选择。

Definition 1 预算集 Budget Set
预算集是在所有选择集中在给定收入$m$下可以负担的起的选择的集合。数学上我们把满足

$$\boldsymbol{x}\boldsymbol{p} \leq m$$

的所有$\boldsymbol{x}$组成的集合叫做预算集。

我们有没有机会将预算线图示出来呢？如果我们用横轴表示商品1的购买数量，纵轴表示商品2的数量，那么我们的预算集应该长这样：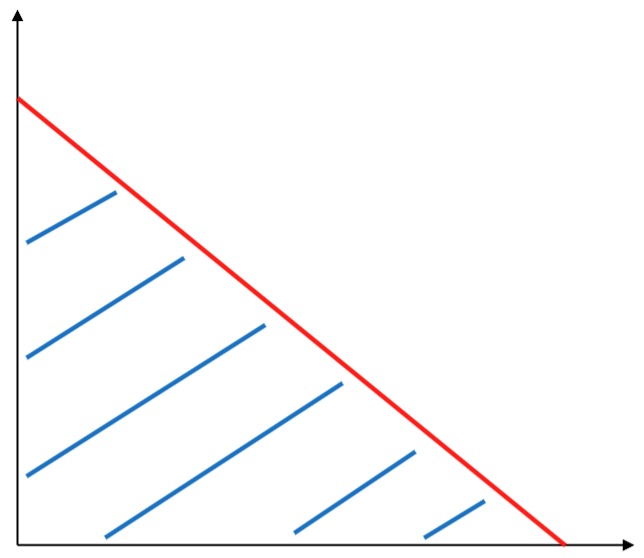

我们又把这个线叫做预算线。预算线有一些性质，但是这对我们理解消费者行为并没有帮助，所以我们略去了。

我们接下来思考几个问题：

1. 预算集和效用有关系吗？
2. 对于不同的收入和价格，预算集可能一样吗？

问题1的答案是否定的，显然我能买什么和我喜欢什么不会有很大的关系；而问题2是肯定的，对于全世界通货膨胀相同的倍数，你能买什么和之前并无区别。

当商品类别不止两个呢？ ​

以商品数量$N = 3$为例画出预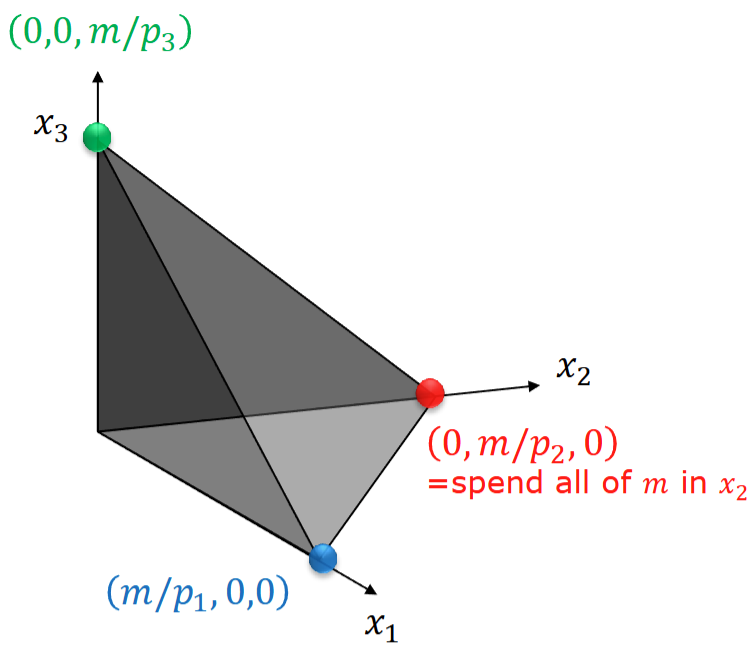算集：

税收对预算集的扭曲 ​

比方说政府征收一个消费税，当我们消费商品1很多个的时候我们会被征收一定的从量税。具体地讲，当$x_1 \geq a$时，对超出的部分征收每单位$t$的税收。我们的预算线会变成什么样子呢？

你可以好好想想再看这个答案

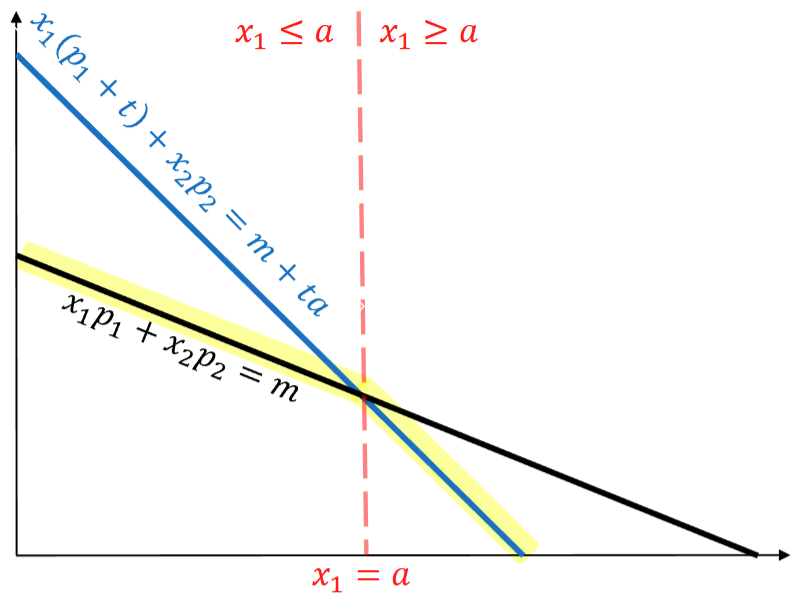
消费者选择问题 Consumer Problem ​

给定效用$U$、收入$m$、价格$p_1,p_2,\cdots, p_n$，我们作为消费者，解决的问题是通过分配收入到不同商品上，来最大化我们的效用，让我们自己最高兴。数学形式上我们把消费者选择问题（往后简称CP）数学上描述如下：

$$\begin{aligned} \max_{x_1,\dots,x_n} \quad & U(x_1,\dots,x_n) \\ \text{s.t.} \quad & x_1 p_1 + \cdots + x_n p_n \le m \\ & x_1 \ge 0,\dots, x_n \ge 0 \end{aligned}$$

透过这个数学形式，如果我们能把上面这个问题解出来，那我们就解决了最大化效用的CP问题。如果有解，我们把这个解记作$x^*$。

无差异曲线 ​

我们的效用函数$U$具有函数的基本特征（什么），所以效用函数应该是可以被画出来的。对于两个商品的情况，我们在一个三维坐标系中可以画出下面的一个示意图：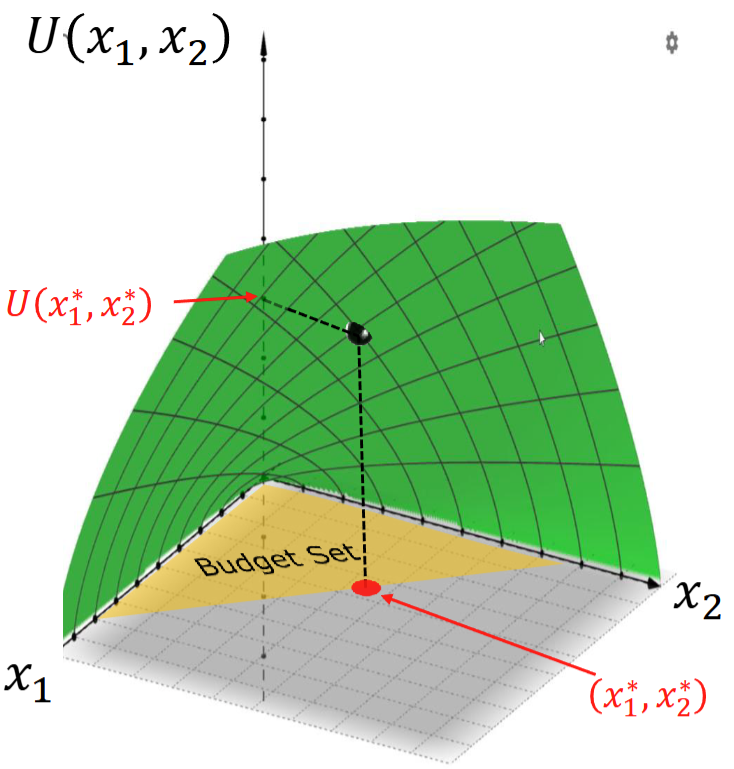

但是我们要的只是$z$轴上的效用，所以不妨思考一下，我们真的需要一个三维的图来解决一个看起来还挺简单的问题吗？

自然是不需要的。我们可以令$U=a$等一系列常数，然后在二维坐标系中画出一系列的曲线来表示一些对我们来说没有差异的选择，我们把这一系列曲线叫做无差异曲线。无差异曲线图示如下：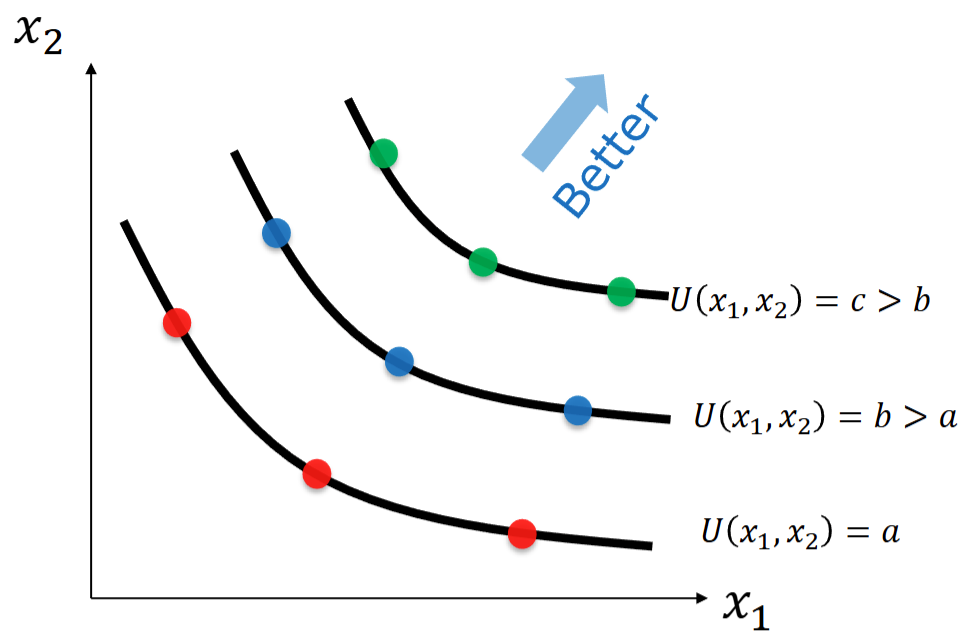

一个很有趣的小定理：

Theorem 1
如果效用函数$U$和$V$表示的是同一偏好$\succcurlyeq$，那么它们的无差异曲线看起来是一样的。

这个定理可以帮助我们画出一些奇形怪状的效用函数的无差异曲线，结合上一讲中的定理，原则上来说各种常见的效用函数的图像已经无法难倒我们了。

CP问题的解 ​

我们接下来进入了求解这个问题的阶段。显然这个问题不是那么好解的，不然选择恐惧症不会存在在这个世上。但是在开始考虑CP问题之前，我们需要考虑几个前置的条件，思考这些条件能帮我们简化接下来的CP问题。

良性偏好 ​

我们研究这个问题的时候总是希望从简单的开始，而简化的模型应当具有一些独特的性质，良性偏好就是最好的性质之一。

Definition 2 良性偏好 Well-Behaved Preference
当一个偏好满足以下两个条件时，我们说一个偏好是良性偏好：

1. 单调性：当某一个商品的消费量增加时，效用增加。或者说，效用函数对每个消费量是单增的。
2. 凸性：对于两个选择$\boldsymbol{x}$和$\boldsymbol{y}$，两个选择的一种混合$\alpha\boldsymbol{x}+(1-\alpha)\boldsymbol{y}$的效用不会比原来某种选择的效用更低。

后面我们把良性偏好简写为WB偏好，或者简单地简称偏好是WB的。

两个必要条件 ​

CP问题有两个必要条件，但是这些条件在我看来并非足够严格，但是确实是直觉上很容易理解。

恰好负担得起 ​

如果我们的效用函数对于至少一个自变量（如$x_i$）是单增的，那么CP问题的解满足$\boldsymbol{x}^* \boldsymbol{p} =m$。

这个的证明是显然的。如果我们花剩了，那就把剩下的钱全部花给$x_i$，这样我们得到的效用一定比原来更高。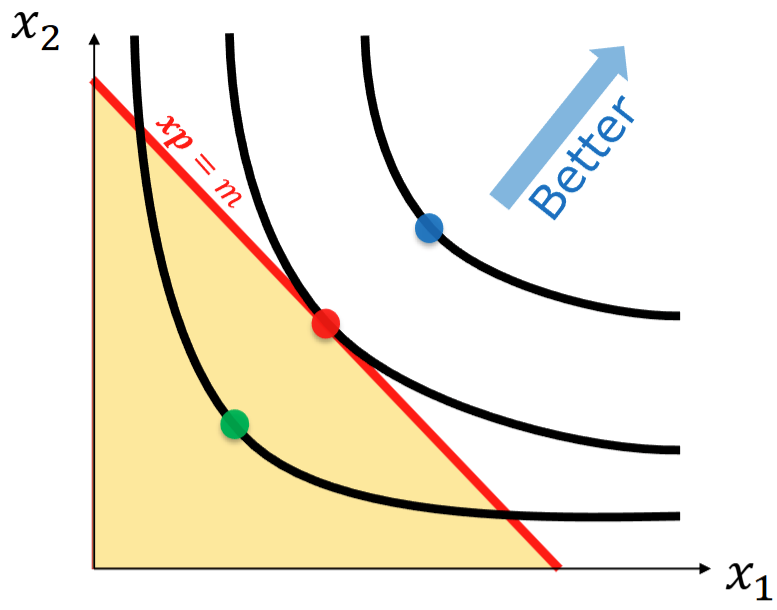

上图是一个简单的图示。当我们处于绿点的时候，我们能负担得起这个消费，但我们并没有达到最大的效用；当我们处于蓝点的时候，我们拥有了更多的效用，但是我们并不能赊账购物！最终我们在反复的抉择中选择了红点，这也确实是CP问题的解。

边际替代率 ​

边际替代率，缩写为MRS。由于边际替代率及相关的计算需要涉及到小学二年级（毕导音）就学过的全微分和相关内容，所以我们略去定义不讲。直观地讲，这个条件指的是如果$x^*$是CP问题的解，那么无差异曲线和预算线相切。

见上图，红点情况下恰好相切。

CP问题求解 ​

回到我们原来的CP问题，经过我们WB的限制后，我们的CP问题阐释变成了这样：

$$\begin{aligned} \max_{x_1,\dots,x_n} \quad & U(x_1,\dots,x_n) \\ \text{s.t.} \quad & x_1 p_1 + \cdots + x_n p_n = m \\ & x_1 \ge 0,\dots, x_n \ge 0 \end{aligned}$$

这个问题的求解在小学二年级学过的高等数学内容中会有介绍，最典型的一个办法是Lagrange方法，这个方法对大部分情况都适用。而当限制了WB之后，我们先前阐述的两个必要条件就变得充分了，所以我们也可以用下列两个式子联立来求解这个问题：

$$\begin{aligned} x_1 p_1 + \cdots + x_n p_n &= m \\ \frac{MU_i(\boldsymbol{x})}{p_i} &= \frac{MU_j(\boldsymbol{x})}{p_j} \end{aligned}$$

虽然我没有介绍边际效用MU，可以简单的理解为对所有商品每单位货币的消费带来的效用增加是相同的。

补充 ​

这些只是CP问题最简单的介绍，上述简化模型的解基本都是内点解（所有商品都消费一定数量，没有商品不消费）。而在更多的时候，我们有一些边角解的情况可能会违反上述的等式，并不是我们的定理出了问题，而是我们人出了问题。比如当预算非常少的时候，或者当某个商品的价格非常高昂的时候，都可能导致边角解的产生。

世界中的偏好也不全是WB的，有些稀奇古怪的偏好会导致解的变化，比如如下对小孩和猫的偏好与求解：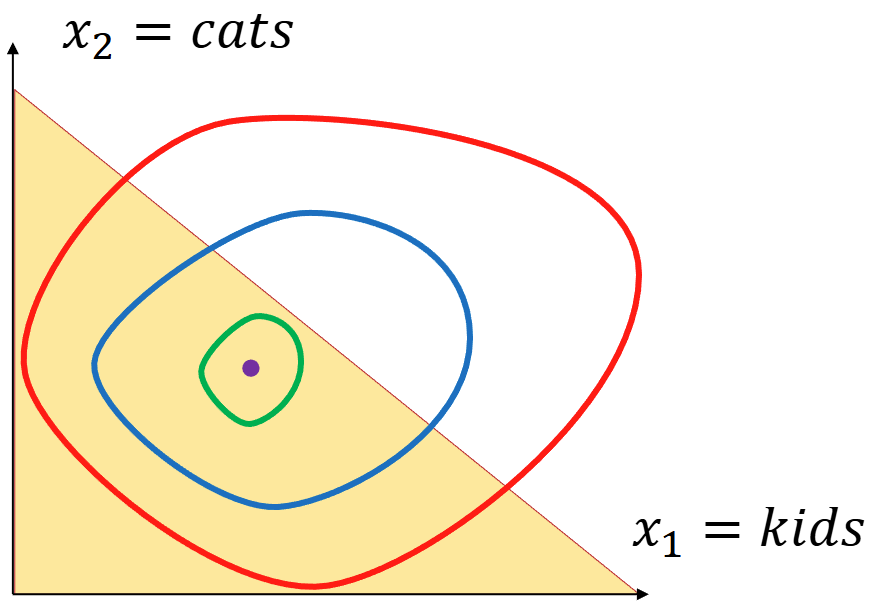

同样是内点解，但是上述的过程并不能解出这个答案，我们需要具体情况具体分析。

CP问题就暂时告一段落了，我们会在不远的将来再次见到最优消费束$x^*$作为一个函数出现，那个时候我们已经在研究市场与均衡了，那都是之后的事情。本次的内容碍于数学的问题无法展开讲述，但如果读者对多元函数求极值比较熟悉的话应该不存在理解上的困难，本质上是将人的偏好量化了之后去理性地求最优，这也是我们01中经济学在干什么着重说明的问题。我们在理性、冷静、克制地看待这个世界。下一次显示偏好则会将这个问题反过来，我们下次再说。